2018. 10. 15. 17:49ㆍML, OpenCV
계단 함수는 계단 모양!
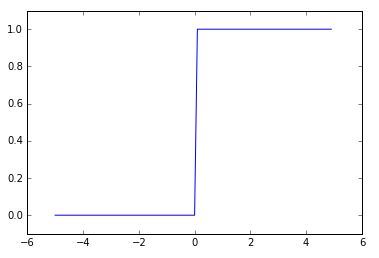
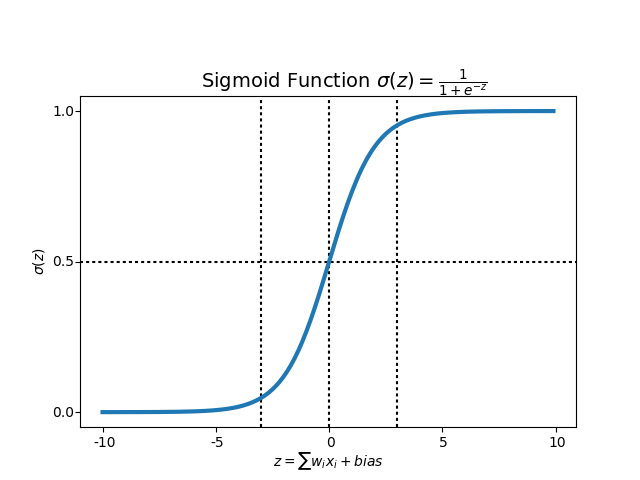
시그모이드(Sigmoid)는 S모양!
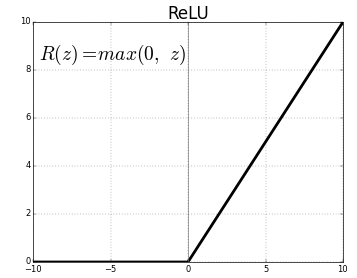
ReLU는 아래와 같이 0보다 큰 값만 나타낸 모양
이제 계단 함수부터 파이썬으로..
|
1
2
3
4
5
6
7
8
9
10
11
|
>>> def step_function(x):
if x > 0:
return 1
else:
return 0
>>> step_function(3)
1
>>> step_function(-0.5)
0
|
cs |
요런 식으로 함수를 만들어주고
x가 0보다 큰 값이 들어오면 1을 반환해주고
그렇지 않으면 0을 반환해주도록 합니다.
0보다 큰 3을 넣었더니 1이 나오고
-0.5를 넣었더니 0이 나오는 것을 확인할 수 있었습니다.,
하지만 입력값을 계속 하나씩 줄 수는 없으니 배열을 사용해봅시다.
|
1
2
3
4
5
6
7
8
9
|
>>> import numpy as np
>>> x = np.array([-0.1,1.0,2.0])
>>> step_function(x)
Traceback (most recent call last):
File "<pyshell#12>", line 1, in <module>
step_function(x)
File "<pyshell#5>", line 2, in step_function
if x > 0:
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
|
cs |
그러면 오류가 발생합니다.
x에 -0.1,1.0,2.0 이라는 배열을 넣어줬는데 오류가 발생했네요.
오류를 해결하기 위해서 bool 형을 활용해 보겠습니다.
bool은 true 혹은 false로 반환됩니다.
|
1
2
3
4
5
6
7
|
>>> import numpy as np
>>> x = np.array([-0.1,1.0,2.0])
>>> x
array([-0.1, 1. , 2. ])
>>> y = x > 0
>>> y
array([False, True, True])
|
cs |
하지만 계단 함수엔는 bool형이 아닌 int형을 사용해서 0과 1로 나타내야 합니다.
그래서 배열 y의 원소를 bool에서 int로 바꿔줍니다.
|
1
2
3
|
>>> y = y.astype(np.int)
>>> y
array([0, 1, 1])
|
cs |
이 방법을 사용해서 계단 함수를 만들어주면
다음과 같습니다.
|
1
2
3
4
5
6
7
|
>>> def step_function(x):
return np.array(x>0,dtype=np.int)
>>> x = np.array([-0.1,1.0,2.0])
>>> y = step_function(x)
>>> y
array([0, 1, 1])
|
cs |
단 두줄로 함수를 정의할 수 있네요.
이제 시그모이드 함수를 구현해봅시다.
|
1
2
3
4
5
6
|
>>> def sigmoid(x):
return 1/(1+np.exp(-x))
>>> x = np.array([-1.0,1.0,2.0])
>>> sigmoid(x)
array([0.26894142, 0.73105858, 0.88079708])
|
시그모이드는 이미 numpy에 있는 exp를 활용하면 간단하게 구현할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
x = np.arange(-5.0,5.0,0.1)
sigmoid(x)
array([0.00669285, 0.00739154, 0.00816257, 0.0090133 , 0.0099518 ,
0.01098694, 0.01212843, 0.01338692, 0.01477403, 0.0163025 ,
0.01798621, 0.01984031, 0.02188127, 0.02412702, 0.02659699,
0.02931223, 0.03229546, 0.03557119, 0.03916572, 0.04310725,
0.04742587, 0.05215356, 0.05732418, 0.06297336, 0.06913842,
0.07585818, 0.0831727 , 0.09112296, 0.09975049, 0.10909682,
0.11920292, 0.13010847, 0.14185106, 0.15446527, 0.16798161,
0.18242552, 0.19781611, 0.21416502, 0.23147522, 0.24973989,
0.26894142, 0.2890505 , 0.31002552, 0.33181223, 0.35434369,
0.37754067, 0.40131234, 0.42555748, 0.450166 , 0.47502081,
0.5 , 0.52497919, 0.549834 , 0.57444252, 0.59868766,
0.62245933, 0.64565631, 0.66818777, 0.68997448, 0.7109495 ,
0.73105858, 0.75026011, 0.76852478, 0.78583498, 0.80218389,
0.81757448, 0.83201839, 0.84553473, 0.85814894, 0.86989153,
0.88079708, 0.89090318, 0.90024951, 0.90887704, 0.9168273 ,
0.92414182, 0.93086158, 0.93702664, 0.94267582, 0.94784644,
0.95257413, 0.95689275, 0.96083428, 0.96442881, 0.96770454,
0.97068777, 0.97340301, 0.97587298, 0.97811873, 0.98015969,
0.98201379, 0.9836975 , 0.98522597, 0.98661308, 0.98787157,
0.98901306, 0.9900482 , 0.9909867 , 0.99183743, 0.99260846])
|
cs |
np.arange를 사용해서 -5.0부터 5.0까지 0.1 간격으로 나타낸 값들을 시그모이드 함수에 넣었더니
위와 같은 값을 얻을 수 있었습니다.
0에 가까운 값에서 1에 가까운 값으로 커지는 것을 알 수 있습니다. (시그모이드는 0과 1 사이의 값을 가진다)
마지막으로 ReLU
더 간단합니다.
파이썬에서 제공하는 np.maximum을 사용하면 됩니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
>>> def relu(x):
return np.maximum(0,x)
>>> x = np.arange(-5.0,5.0,0.1)
>>> relu(x)
array([0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0.1,
0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. , 1.1, 1.2, 1.3, 1.4,
1.5, 1.6, 1.7, 1.8, 1.9, 2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7,
2.8, 2.9, 3. , 3.1, 3.2, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4. ,
4.1, 4.2, 4.3, 4.4, 4.5, 4.6, 4.7, 4.8, 4.9])
|
cs |
시그모이드 때와 같이
np.arrange를 사용해서 -5.0부터 5.0까지 0.1 간격으로 나타낸 값들을 시그모이드 함수에 넣었더니
0.1부터 값이 늘어나고 0보다 작은 값들은 모두 0으로 나타내 줍니다.